Lamberts W-funktion

Graf av W₀(x) för -1/e ≤ x ≤ 4

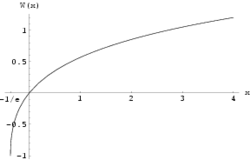
Lamberts W-funktion är en matematisk funktion som används för att lösa ekvationer innehållande logaritmer eller exponentialfunktioner som inte kan elimineras algebraiskt. Den betecknas W och definieras som inversen till funktionen

$f(w)=w{e}^w$

där w är ett komplext tal och e^w betecknar exponentialfunktionen. Lamberts W-funktion är uppkallad efter den schweizisk-preussiske matematikern och fysikern Johann Heinrich Lambert.

Flervärdhet

Funktionen

$f(w)=w{e}^w$

är inte injektiv på (−∞, 0) och W är därför en flervärd funktion på [−1/e, 0). För reella argument x ≥ −1/e kan man med kravet w ≥ −1 definiera en entydig funktion W₀. Denna funktion uppfyller W₀(0) = 0 och W₀(−1/e) = −1.

Metod för ekvationslösning

Lamberts W-funktion uppfyller

$z=W(z)e^{W(z)}$

och kan därför tillämpas genom att man skriver om ekvationer på formen $c=x{e}^x$ där c är konstant, varefter lösningen ges av $x=W(c)$. Exempelvis kan ekvationen 2^t = 5t lösas genom omskrivningen

$2^t=5t\Rightarrow$

$1=5t{e}^{-t\log 2}\Rightarrow$

$\frac{-\log 2}{5}=(-t\log 2)e^{(-t\log 2)}\Rightarrow$

$-t\log 2=W\left(\frac{-\log 2}{5}\right)\Rightarrow$

$t=\frac{-W\left(\frac{-\log 2}{5}\right)}{\log 2}.$

Specifika ekvationer och värden

De ekvivalenta ekvationerna $x=\log x$ och $x=e^x$ har lösningen

$x=-W(-1)\approx 0,31813-1,33724i.$

Ekvationen $x^x=z$ löses av

$x=\frac{\log z}{W(\log z)}=\exp (W(\log z)),$

och det oändliga tornet av potenser

$c=z^{z^{z^{\cdots }}}$

antar vid konvergens värdet

$c=\frac{W(-\log z)}{-\log z}.$

Några specifika värden är

$W(-\pi /2)=i\pi /2$

$W(-\frac{\ln a}{a})=-\ln a(\frac{1}{e}\le a\le e)$

$W(-1/e)=-1$

$W(-\log 2/2)=-\log 2$

$W(0)=0$

$W(e)=1$

$W(1)=\mathrm{\Omega }$ (omegakonstanten)

$W(-1)\approx -0.31813-1.33723\mathrm{i}$

$W^{\prime }\left(0\right)=1$.

Taylorserie

Maclaurinserien till Lamberts W-funktion kan beräknas utifrån den implicita ekvationen

$z=W(z)e^{W(z)}$

genom Lagranges inverteringssats. Resultatet är

$W_0(x)=\sum _{n=1}^{\mathrm{\infty }}\frac{(-n{)}^{n-1}}{n!}{x}^n=x-x^2+\frac{3}{2}{x}^3-\frac{8}{3}{x}^4+\frac{125}{24}{x}^5-\cdots$

som enligt kvottestet har konvergensradien 1/e.

Mer allmänt, för $r\in \mathbb{Z},$ är

$W_0(x{)}^r=\sum _{n=r}^{\mathrm{\infty }}\frac{-r(-n{)}^{n-r-1}}{(n-r)!}{x}^n.$

Derivata och primitiv funktion

Derivatan ges av

$\frac{d}{dx}W(x)=\frac{W(x)}{x(1+W(x))}$.

Många uttryck innehållande Lamberts W-funktion kan integreras genom variabelsubstitutionen w = W(x), det vill säga x = w e^w. Speciellt gäller

$\int W(x)dx=x(W(x)-1+\frac{1}{W(x)})+C.$

Differentialekvation

Lamberts W-funktion uppfyller differentialekvationen

$z(1+W)\frac{dW}{dz}=Wz\ne -1/e.$

Övriga formler

$\underset{0}{\overset{\pi }{\int }}W(2{\cot }^2(x)){\sec }^2(x)\mathrm{d}x=4\sqrt{\pi }$

$\underset{0}{\overset{\mathrm{\infty }}{\int }}W\left(\frac{1}{x^2}\right)\mathrm{d}x=\sqrt{2\pi }$

$\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{W(x)}{x\sqrt{x}}\mathrm{d}x=2\sqrt{2\pi }$

Tillväxt

En approximation av $W_0(x)$ för stora $x$ är

$W_0(x)=\ln x-\ln \ln x+\frac{\ln \ln x}{\ln x}+O\left({\left(\frac{\ln \ln x}{\ln x}\right)}^2\right).$

Externa länkar

• Mall:Commonscat