Fixpunkt (matematik)

En funktion med tre (synliga) fixpunkter.

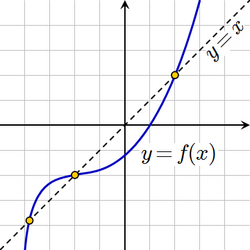
Inom matematiken är en fixpunkt till en funktion en punkt som avbildas på sig själv, det vill säga en punkt $a$ sådan att $f(a)=a$ är en fixpunkt till $f(x)$.

För att hitta fixpunkter till en funktion $f(x)$ kan man lösa ekvationen $f(x)=x$.

Alla funktioner har inte fixpunkter, exempelvis är $f(x)=x-1$ fixpunktslös. I det fallet beskriver funktionen en linje som är parallell med linjen $y=x$ och linjerna kommer därför aldrig att mötas.

Attraktiva fixpunkter

Fixpunktsiteration för cosinus med begynnelsevärde -1

En attraktiv fixpunkt till en funktion $f$ är punkt $x_0$ sådan att för varje $x$ i definitionsmängden till $f$ som är tillräckligt nära $x_0$ så konvergerar serien:

$x,f(x),f(f(x)),f(f(f(x))),...$

till $x_0$.

Cosinus har en fixpunkt och den är attraktiv. "Tillräckligt nära" i det här fallet innebär alla reella tal. Serien kommer för cosinus att konvergera mot 0,73909... Dock är inte alla fixpunkter attraktiva, till exempel så har funktionen $f(x)=2x$ en fixpunkt i $x_0=0$, men i alla närheter av $x_0$ (förutom just i $x_0$) kommer funktionen att avlägsna sig från $x_0$ istället för att närma sig.

En fixpunkt $x_0$ är garanterat attraktiv om $f$ är kontinuerligt deriverbar i en omgivning till $x_0$ och $|f{}^{\prime }(x_0)|<1$,

Fixpunktssatser

Det finns många fixpunktssater som garanterar att det finns en fixpunkt till en funktion under vissa omständigheter. Exempelvis Brouwers fixpunktssats och Borels fixpunktssats

Relaterade koncept

• Egenvektor
• Idempotent
• Invariant