De Morgans lagar

Mall:Logiskafunktioner2 De Morgans lagar är två slutledningsregler inom logik och boolesk algebra, uppkallade efter Augustus de Morgan på 1800-talet. Lagarna var kända redan på medeltiden och formulerades språkligt av William Ockham på 1400-talet. Reglerna, uttryckta som tautologier eller som teorem inom satslogiken, är

$\begin{array}{cc}\mathrm{\neg }(P\wedge Q)& \to \mathrm{\neg }P\vee \mathrm{\neg }Q\\ \mathrm{\neg }(P\vee Q)& \to \mathrm{\neg }P\wedge \mathrm{\neg }Q\end{array}$

där $P$ och $Q$ är påståenden. Den första regeln är en negation av en konjunktion och den andra, en negation av en disjunktion.

Informellt kan lagarna skrivas

inte (P och Q) = inte P eller inte Q

inte (P eller Q) = inte P och inte Q

Reglerna har motsvarigheter inom mängdläran:

$(A\cap B{)}^{\complement }=A^{\complement }\cup B^{\complement }$

$(A\cup B{)}^{\complement }=A^{\complement }\cap B^{\complement }$

där ∩ är snittoperatorn och ∪ är unionsoperatorn.

Den allmänna formen är

$\begin{array}{cc}\overline{\bigcap _{i\in I}{A}_i}& \equiv \bigcup _{i\in I}\overline{A_i},\\ \overline{\bigcup _{i\in I}{A}_i}& \equiv \bigcap _{i\in I}\overline{A_i},\end{array}$

där Mall:Math är en indexmängd och $\bar{A}$ är A:s negation.

De Morgans lagar har tillämpningar inom digitaltekniken vid konstruktion av logiska kretselement. De Morgans lagar motsvaras av logiska grindar enligt (1 = hög nivå, 0 = låg nivå):

	=			$A$	$B$	$\mathrm{\neg }(A\wedge B)$	$\mathrm{\neg }A\vee \mathrm{\neg }B$
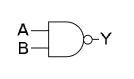0	0	1	1
0	1	1	1
1	0	1	1
1	1	0	0

|}

	=			$A$	$B$	$\mathrm{\neg }(A\vee B)$	$\mathrm{\neg }A\wedge \mathrm{\neg }B$
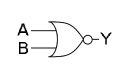0	0	1	1
0	1	0	0
1	0	0	0
1	1	0	0

|}

Referenser

• Karl-Johan Bäckström, Diskret matematik, Studentlitteratur, Lund 1986.
• Raymond M Smullyan, First-Order Logic, Springer-Verlag, Berlin Heidelberg, New York, 1968.
• Elliott Mendelson, Elementary Logic, Oxford University Press, London 1965.
• Göran Hermerén, Satslogik, Studentlitteratur, Lund 1967.
• Per-Erik Danielsson, Digital teknik, Studentlitteratur, Lund 1974.