Spegelekvationen

Spegelekvationen används inom Optiken för att beräkna storleken på den virtuella bilden i en spegel.

Spegelekvationen för sfäriska speglar

Då ett föremål $A$ avbildas i en sfärisk spegel kommer avbilden $B$ av föremålet att hamna på ett läge som S. förutsäger. $B$:s läge och orientering beror på hur föremålet är placerat i förhållande till spegelns krökningscentrum $C$ och brännpunkt $F$. Alla beteckningar enligt nedanstående figur.

Med nedanstående bilds beteckningar lyder S. enligt följande: $\frac{1}{a}+\frac{1}{b}=\frac{1}{f}$

Sfärisk spegel med ingående beteckningar

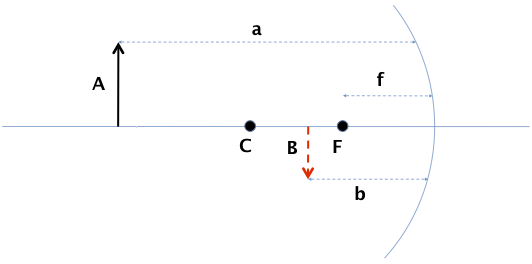
Tecken på avståndsvariabler och brännvidd

• $a>0$ då A är placerad framför spegelytan
• $b<0$ då B avbildas bakom spegelytan (dvs. avbildningen är en virtuell bild)
• $f>0$ då spegeln är konkav
• $f<0$ då spegeln är konvex

Förstoring

Endimensionellt fall

Om A:s och B:s storlekar definieras enligt |A| respektive |B| gäller att förstoringen på avbilden definieras enligt

$M=\frac{|B|}{|A|}=\frac{b}{a}$

• $M<0$ då orienteringen på avbilden är skiftad med 180 grader jämfört med föremålet som avbildas
• $M>0$ då orienteringen på avbilden är densamma som föremålet som avbildas