Schläfli-symbol

En dodekaeder har Schläfli-symbolen $\{5,3\}$, det vill säga att tre regelbundna femhörningar möts i varje hörn.

Mall:Dubbel bild Mall:Dubbel bild Schläfli-symbolen, uppkallad efter den schweiziske matematikern Ludwig Schläfli, är en notation på formen $\{p,q,r,\dots \}$ som används för att beskriva regelbundna polygoner, polyedrar, polytoper och tessellationer.

Om $p$ är ett naturligt tal betecknar Schläfli-symbolen $\left\{p\right\}$ en regelbunden polygon, en $p$-hörning.

Är $p$ ett oreducerbart heltalsbråk $p=\frac{a}{b}$ betecknar $\left\{\frac{a}{b}\right\}$ en regelbunden stjärnpolygon med $a$ hörn, där $b$ anger till vilket hörn en sida ansluter. $\left\{\frac{5}{2}\right\}$ är alltså en femhörnig stjärnpolygon (ett pentagram), medan $\left\{\frac{5}{1}\right\}=\left\{5\right\}$, det vill säga en vanlig regelbunden femhörning.

Schläfli-symbolen $\{p,q\}$ betecknar en kropp eller tessellation bestående av regelbundna $p$-hörningar (eller om det är ett bråk regelbundna stjärnpolygoner) där $q$ anger hur många sådana som möts i varje hörn (eller snarare vilken vertexfigur hörnet har).

En inversion av Schläfli-symbolen, det vill säga att elementen anges i omvänd ordning, ger den duala polytopen. Så anger exempelvis $\{4,3\}$ en kub och $\{3,4\}$ en oktaeder, som är kubens duala polyeder. På samma sätt är $\{6,3\}$ tessellationen av planet med regelbundna sexhörningar och dess dual $\{3,6\}$ tessellationen av planet med liksidiga trianglar. Om Schläfli-symbolen för en figur är symmetrisk under inversion innebär det att figuren är självdual; som tessellationen av planet i kvadrater $\{4,4\}$ eller tetraedern $\{3,3\}$.

I två dimensioner finns det de tre nyssnämnda tessellationerna av planet med liksidiga trianglar $\{3,6\}$, kvadrater $\{4,4\}$ och regelbundna sexhörningar $\{6,3\}$

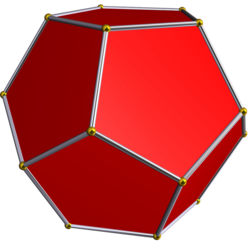
De regelbundna tredimensionella polyedrarna utgörs av de fem konvexa platonska kropparna: tetraeder $\{3,3\}$, kub $\{4,3\}$ och dess dual oktaeder $\{3,4\}$, samt dodekaeder $\{5,3\}$ och dess dual ikosaeder $\{3,5\}$. Därutöver finns det de fyra konvexa Kepler-Poinsot-kropparna: Liten stjärndodekaeder $\{\frac{5}{2},5\}$ med dualen stor dodekaeder $\{5,\frac{5}{2}\}$ och stor stjärndodekaeder $\{\frac{5}{2},3\}$ med dualen stor ikosaeder $\{3,\frac{5}{2}\}$.

Fyrdimensionella regelbundna polytoper har Schläfli-symbolen $\{p,q,r\}$ där $p$ och $q$, liksom i det tredimensionella fallet, betecknar att $q$ stycken $p$-hörningar möts i varje hörn, medan $r$ betecknar att $r$ stycken $\{p,q\}$-volymer möts längs varje kant. En fyrdimensionell simplex betecknas sålunda $\{3,3,3\}$ och en tesserakt $\{4,3,3\}$. En simplex är självdual, medan den duala polytopen till tesserakten, som har Schläfli-symbolen $\{3,3,4\}$ och kallas 16-cell eller hexadekakor, består av tetraedrar, $\{3,3\}$, som fyra och fyra möts längs varje kant. Utöver dessa tre finns det tre ytterligare regelbundna konvexa polytoper av dimension fyra: den självduala 24-cellen och det duala paret 120-cellen och 600-cellen med Schläfli-symbolerna $\{3,4,3\}$, $\{5,3,3\}$ respektive $\{3,3,5\}$. Därutöver finns det tio regelbundna konkava stjärnpolytoper av dimension fyra.

För regelbundna polytoper av högre dimension ($n$) tillkommer ett element i symbolen för varje ytterligare dimension. Detta element anger hur många objekt av dimension $n-1$ som möts vid varje objekt av dimension $n-3$. En $n$-dimensionell hyperkub har sålunda Schläfli-symbolen $\{4,3,...,3\}$ med $n-2$ treor. $n$-hyperkuben, dess dual ($n$-hyperoktaedern, $n$-ortoplexen eller $n$-korspolytopen) $\{3,3,...,3,4\}$ och den självduala $n$-simplexen $\{3,3,...,3\}$ är de enda regelbundna polytoperna av dimension fem eller högre. De är samtliga konvexa.

Referenser och noter

• Eric Weisstein, Schläfli symbol på Wolfram MathWorld.