Integralkalkyl

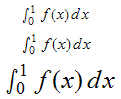
Integralkalkyl är själva uträkningen av specifika integraler. För enklare integraler kan detta ofta göras direkt med hjälp av resultaten från analysens huvudsats, medan mer komplicerade fall kan kräva partiell integrering eller Fourieranalys.

Analysens huvudsats

Mall:Huvudartikel Sats: Om en funktion f är kontinuerlig i intervallet [a,b] och x är ett tal i intervallet [a,b] så är

$S(x)=\underset{a}{\overset{x}{\int }}f(t)dt$

en primitiv funktion till f, det vill säga funktionen S är deriverbar med S'(x) = f(x). Analysens huvudsats gör det möjligt att derivera parameterberoende integraler av formen

$\underset{a}{\overset{b}{\int }}f(t)dt$.

Insättningsformeln

Insättningsformeln följer direkt ur analysens huvudsats, och används i all integralkalkyl.

Sats: Om en funktion f är kontinuerlig i [a,b] och F är en primitiv funktion till f så är

$\underset{a}{\overset{b}{\int }}f(t)dt=F(b)-F(a).$

Exempel: Arean under grafen till funktionen Mall:Nowrap på intervallet [2,4] är

$\underset{2}{\overset{4}{\int }}{x^2+2xdx=\left[\frac{x^3}{3}+x^2\right]}_2^4=(\frac{4^3}{3}+4^2)-(\frac{2^3}{3}+2^2)=\frac{92}{3}.$

Med insättningsformeln kan även integraler på formen

$S(x)=\underset{a}{\overset{f(x)}{\int }}g(t)dt$

deriveras enligt

$\frac{dS}{dx}(x)=\frac{d}{dx}(G(f(x))-G(a))=g(f(x))\frac{df}{dx}(x).$

Se även

• Integral
• Riemannintegral
• Derivata

Externa länkar

• Mall:Commonscat