Födelse- och dödsprocess

Mall:Källor Födelse- och dödsprocess är en speciell stokastisk process i kontinuerlig tid med de icke-negativa heltalen som tillstånd och där de enda förändringarna är födelse och död vilket innebär att man tar ett steg uppåt eller nedåt i tillstånden. Processen har viktiga tillämpningar inom flera områden bl.a. inom demografi för att modellera en folkmängd där invånarna dör och föds, därav den stokastiska processens namn. Det finns även viktiga tillämpningar inom biologi där man beskriver bakterieodlingar, i köteori för att beskriva antalet kunder i en kö och inom epidemiologi för att beskriva antalet smittade i en befolkning.

Matematisk beskrivning

En födsel innebär att tillståndet förändras från i till i + 1 medan en död innebär att tillståndet går från i till i - 1. Processen beskrivs med födelsetal $\{{\lambda }_i{\}}_{i=0\dots \mathrm{\infty }}$ och dödstal 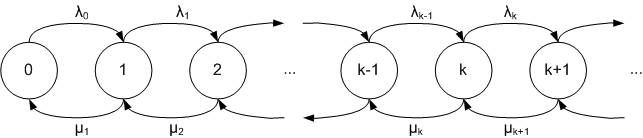$\{{\mu }_i{\}}_{i=1\dots \mathrm{\infty }}$

En ren födelseprocess är en födelse- dödsprocess där ${\mu }_i=0$ för alla $i\ge 0$.

En ren dödsprocess är en födelse- dödsprocess där ${\lambda }_i=0$ för alla $i\ge 0$.

Användning i köteori

Ett av de direkta användningsområdena för födelse- dödsprocess är i kösystem.

För en kö födelse- dödsprocess gäller att

1. När processen befinner sig i tillstånd i ansluter sig kunder som en Poissonprocess med takten ${\lambda }_i$.
2. Successiva tider mellan anslutningar till kön är exponentiella slumpmässiga variabler. När processen är i tillstånd i har den slumpmässiga variabeln parametern ${\lambda }_i$.
3. Successiva betjäningstider är exponentiella slumpmässiga variabler. När processen är i tillstånd i har den slumpmässiga variabeln parametern ${\mu }_i$.

M/M/1 queue

M/M/1-kön har oändlig längd och är en enkel betjäningskö, alltså endast person längst fram kan bli betjänad. I en ickeslumpmässig omgivning tenderar föddelse- dödsprovessen i kömodeller att bli genomsnitt för en lång tid. Den genomsnittliga takten på anslutning ges av $\lambda$ och den genomsnittliga betjäningstiden ges av $1/\mu$. Födelse- dödsprocessen är en M/M/1-kö när

${\lambda }_i=\lambda \text{ och }{\mu }_i=\mu \text{ för alla }i.$

Differentialekvation för sannolikheten att processen är i tillståndet k vid tid t är,

$p_0^{\prime }(t)={\mu }_1{p}_1(t)-{\lambda }_0{p}_0(t)$

$p_k^{\prime }(t)={\lambda }_{k-1}{p}_{k-1}(t)+{\mu }_{k+1}{p}_{k+1}(t)-({\lambda }_k+{\mu }_k)p_k(t)$

M/M/c queue

M/M/c kön har oändlig längd och är en mångbetjäningskö med C stycken kanaler, alltså C kunder kan få service samtidigt. Det enda som separerar den från M/M/1-kön är servicetiden som nu blir

${\mu }_i=i\mu \text{ för }i\le C$

och

${\mu }_i=C\mu \text{ för }i\ge C$

då

${\lambda }_i=\lambda \text{ för alla }i.$

Användning för att modellera befolkningsutveckling

En linjär födelse- och dödsprocess kan till exempel beskriva hur arter eller populationer utvecklas. Nybildning och utdöd av de individer som processen representerar är proportionell mot antal individer. Födelse- respektive dödstakten för hela processen är $\lambda X(t)$ och $\mu X(t)$, där $X(t)$ representerar tillståndet, det vill säga antal individer. Parametrarna $\lambda$ och $\mu$ är konstanter.

$p_k(t)$ representerar sannolikheten att processen vid tiden $t$ innehåller $k$ individer, alltså $p_k(t)=P(X(t)=k)$, där $X(t)$ är en stokastisk process.

Parametrarna $\lambda$ och $\mu$ representerar takten varmed en enskild individ föds respektive dör. Vi vill beskriva sannolikheten att vi har $k$ individer vid tiden $t+\mathrm{\Delta }t$, alltså $X(t+\mathrm{\Delta }t)=k$. Det finns olika sätt att härleda processen $X(t+\mathrm{\Delta }t)=k$. I denna härledning utgår vi ifrån att det finns följande olika sätt för processen att hamna på $X(t)=k$ under tidssteget.

1. Det finns $k$ individer och ingenting händer under tidssteget $\mathrm{\Delta }t$.
2. Det finns $k-1$ individer och en ny individ bildas under tidssteget $\mathrm{\Delta }t$.
3. Det finns $k+1$ individer och en individ dör ut under tidssteget $\mathrm{\Delta }t$.
4. Det finns $k\pm n$ och n individer bildas/dör ut under tidssteget $\mathrm{\Delta }t$.

För godtyckligt små $\mathrm{\Delta }t$ kommer då följande ekvation att gälla.

$p_k(t+\mathrm{\Delta }t)=\stackrel{1}{\overbrace{p_k(t)(1-(k\lambda +k\mu )\mathrm{\Delta }t)}}+\stackrel{2}{\overbrace{p_{k-1}(t)\lambda (k-1)\mathrm{\Delta }t}}+\stackrel{3}{\overbrace{p_{k+1}(t)\mu (k+1)\mathrm{\Delta }t}}+\stackrel{4}{\overbrace{𝒪(\mathrm{\Delta }{t}^2)}}$

Högerledets första term representerar sannolikheten att ingenting händer under tidssteget. Den andra termen representerar sannolikheten att en individ dör ut och den tredje att en ny individ bildas. Ordo-termen representerar att fler än en händelse förekommer under tiden $\mathrm{\Delta }t$. Genom att subtrahera $p_k(t)$ och dividera båda leden i ekvationen med $\mathrm{\Delta }t$ och låta $\mathrm{\Delta }t\to 0$ får vi en differens- differentialekvation för $p_k(t)$ i tidpunkten $t$.

${p_k}^{\prime }(t)=-k(\lambda +\mu )p_k(t)+\lambda (k-1)p_{k-1}(t)+\mu (k+1)\mu p_{k+1}(t)$

Eftersom $\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{𝒪(\mathrm{\Delta }{t}^2)}{\mathrm{\Delta }t}\to 0$ kommer sannolikheten att det sker mer än en födelse- eller dödshändelse samtidigt vara noll. För att kunna uttrycka den önskvärda sannolikheten $p_k$ behöver ekvationen lösas vilket görs genom att multiplicera ekvationen med $s^k$ och summera över alla möjliga $k$.

$\sum _{k=0}^{\mathrm{\infty }}{s}^k{p_k}^{\prime }(t)=\lambda s^2\sum _{k=2}^{\mathrm{\infty }}(k-1)s^{k-2}{p}_{k-1}(t)-(\lambda +\mu )s\sum _{k=1}^{\mathrm{\infty }}k{s}^{k-1}{p}_k(t)+\mu \sum _{k=0}^{\mathrm{\infty }}(k+1)s^k{p}_{k+1}(t)$

Ovanstående uttryck innehåller den sannolikhetsgenererande funktionen samt dess derivator. På så sätt erhålls en partiell differentialekvation

$\frac{\partial G}{\partial t}=\lambda s^2\frac{\partial G}{\partial s}-(\lambda +\mu )s\frac{\partial G}{\partial s}+\mu \frac{\partial G}{\partial s}=(\lambda s-\mu )(s-1)\frac{\partial G}{\partial s}$

Begynnelsevärdet får man genom att betrakta den sannolikhetsgenererande funktionen utifrån dess tidsberoende.

$G(s,0)=\sum _{k=0}^{\mathrm{\infty }}{s}^{k}P(X(0)=k)=s^{X(0)}$

Sista steget är en följd av att $P(X(0)=k)=0$ för alla $k\ne X(0)$, där $X(0)$ är det antal individer som existerar vid $t=0$.

Lösningen till den partiella differentialekvationen erhålls till exempel med karakteristiska metoden.

$G(s,t)=\{\begin{array}{cc}(\frac{\lambda t(1-s)+s}{\lambda t(1-s)+1}{)}^{X(0)},& \mu =\lambda \\ (\frac{\mu (1-s)-(\mu -\lambda s)e^{-t(\lambda -\mu )}}{\lambda t(1-s)-(\mu -\lambda s)e^{-t(\lambda -\mu )}}{)}^{X(0)},& \mu \ne \lambda \end{array}$

Den sannolikhetsgenererande funktionen för födelse- och dödsprocessen är en kvot av två linjära funktioner, vilket gör att man kan använda en så kallad Bruten linjär fördelning för att beskriva processen. Alla sannolikhetsfördelningar vars genererande funktion kan skrivas som en kvot av två linjära funktioner följer en bruten linjär fördelning med parametrar $p_0$ och $p$.

$P(X(t)=k)=\{\begin{array}{cc}{p}_0,& k=0\\ (1-p_0)p(1-p{)}^{k-1},& k>0\end{array}$

Multiplicerar man uttrycket för $P(X(t)=k)$ med $s^k$ och summerar över alla $k$ kan parametrarna $p_0$ och $p$ uttryckas med hjälp av den sannolikhetsgenererande funktionen.

$G(s,t)=\sum _{k=0}^{\mathrm{\infty }}{s}^k{p}_k(t)=p_0+\sum _{k=1}^{\mathrm{\infty }}{s}^k(1-p_0)p(1-p{)}^{k-1}=p_0+(1-p_0)p\sum _{k=0}^{\mathrm{\infty }}{s}^k(1-p{)}^k=p_0+(1-p_0)\frac{ps}{1-s(1-p)}$

Parametrarna $p_0$ och $p$ är funktioner av tid, men kan behandlas som konstanter med avseende på variablerna $s$ och $k$. Vid varje tidpunkt kommer processen att följa den brutna linjära fördelningen. Parametern $p_0$ faller ut ur den genererande funktionen i punkten $s=0$, enligt följande ekvation.

$G(0,t)=\underset{s\to 0}{\lim }(p_0+(1-p_0)\frac{ps}{1-s(1-p)})=p_0$

Eftersom man kan uttrycka den sannolikhetsgenererande funktionen för processen, $G(s,t)$ får vi därför följande uttryck för $p_0$.

$p_0(t)=G(0,t)=\{\begin{array}{cc}\frac{\lambda t}{(\lambda t+1)},& \mu =\lambda \\ \frac{\mu (e^{t(\lambda -\mu )}-1)}{\lambda e^{t(\lambda -\mu )}-\mu },& \mu \ne \lambda \end{array}$

För att beräkna $p$ använder vi.

$G(s,t)=p_0+(1-p_0)\frac{ps}{1-s(1-p)}\iff p=\frac{(1-s)(p_0-G(s,t))}{s(G(s,t)-1)}$

Använder man den sannolikhetsgenererande funktionen för processen, samt parametern $p_o$ fås parametern $p$.

$p(t)=\{\begin{array}{cc}\frac{1}{1+\lambda t},& \mu =\lambda \\ \frac{\lambda -\mu }{\lambda e^{t(\lambda -\mu )}-\mu },& \mu \ne \lambda \end{array}$

Genom att använda de explicita uttrycken för parametrarna $p_0(t)$ och $p(t)$ fås sammanfattningsvis ett analytiskt uttryck för att beskriva sannolikheten att $k$ individer existerar vid tiden $t$, givet födelsetakten $\lambda$ och dödstakten $\mu$.

$P(X(t)=k)=\{\begin{array}{cc}\frac{\lambda t}{\lambda t+1},& \mu =\lambda ,k=0\\ \frac{(\lambda t{)}^{k-1}}{(\lambda t+1{)}^{k+1}},& \mu =\lambda ,k>0\\ \frac{\mu (e^{t(\lambda -\mu )}-1)}{\lambda e^{t(\lambda -\mu )}-\mu },& \mu \ne \lambda ,k=0\\ \frac{(\lambda -\mu {)}^2{e}^{t(\lambda -\mu )}{\lambda }^{k-1}(e^{t(\lambda -\mu )}-1{)}^{k-1}}{(\lambda e^{t(\lambda -\mu )}-\mu {)}^{k+1}},& \mu \ne \lambda ,k>0\end{array}$

Jämviktsläge

En kö sägs vara i jämviktsläge om gränsen $\underset{t\to \mathrm{\infty }}{\lim }{p}_k(t)$ existerar. Om detta ska gälla måste $p_k^{\prime }(t)$ vara lika med noll. Vi använder M/M/1-kön som exempel, det stabila tillståndet (jämviktslägets) ekvationer är,

${\lambda }_0{p}_0(t)={\mu }_1{p}_1(t)$

$({\lambda }_k+{\mu }_k)p_k(t)={\lambda }_{k-1}{p}_{k-1}(t)+{\mu }_{k+1}{p}_{k+1}(t)$

Om ${\lambda }_k=\lambda$ och ${\mu }_k=\mu$ för alla $k$ (Det homogena fallet), detta kan reduceras till

$\lambda p_k(t)=\mu p_{k+1}(t)\text{ for }k\ge 0.$