Fil:Regression pic assymetrique.gif
Från testwiki
Hoppa till navigering
Hoppa till sök
Regression_pic_assymetrique.gif (610 × 460 pixlar, filstorlek: 22 kbyte, MIME-typ: image/gif, upprepad, 10 bildrutor, 5,0 s)
Den här filen är från Wikimedia Commons och kan användas av andra projekt. Beskrivningen på dess filbeskrivningssida där visas nedan.
Sammanfattning
| BeskrivningRegression pic assymetrique.gif |
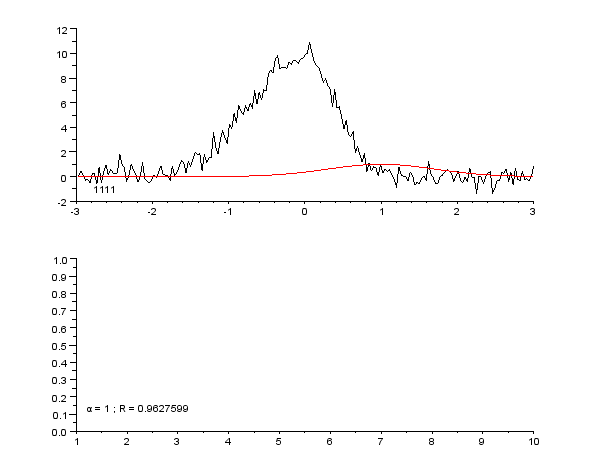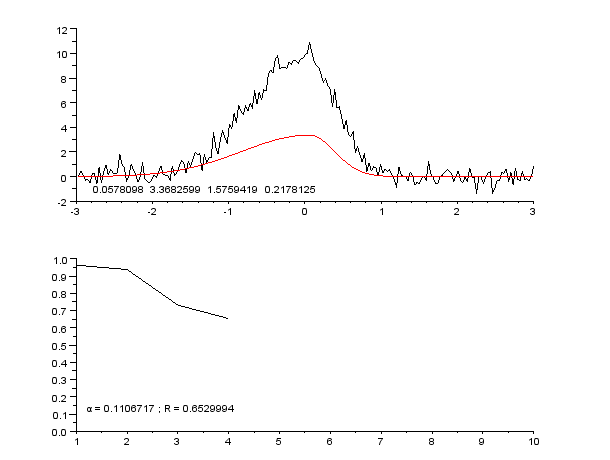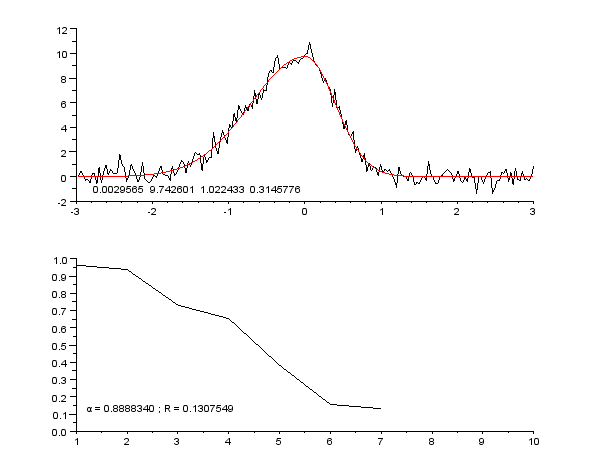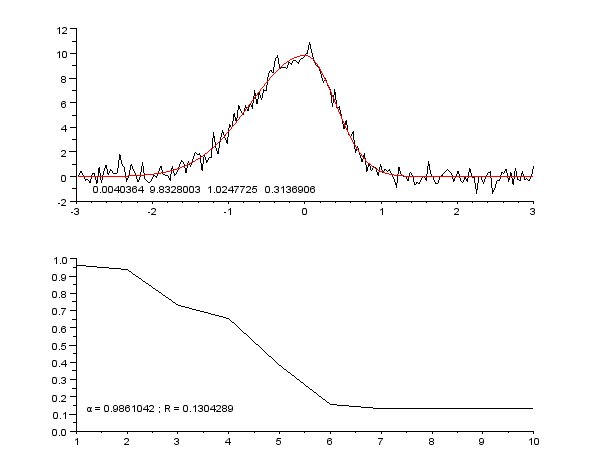
English: Successive steps of Gauss-Newton regression, with variable damping factor α, to fit a dissymetrical noisy peak.
Pictures created with Scilab, animated with The Gimp.
Français : Étapes successives d'une régression de Gauss-Newton, avec facteur d'amortissement α variable, pour ajuster un pic assymétrique.
Images créées avec Scilab ; animation créée avec The Gimp. |
| Datum | |
| Källa | Eget arbete |
| Skapare | Cdang (Christophe Dang Ngoc Chan) |
Scilab source
| This media was created with Scilab, a free open-source software. Here is a listing of the Scilab source used to create this file. |
Le fichier de données et celui de fonctions communes sont identiques à ceux de File:Regression pic gaussien dissymetrique bruite.svg.
// **********
// Constantes et initialisation
// **********
clear;
clf;
chdir('monchemin/')
// Paramètres de Newton-Raphson
precision = 1e-7; // condition d'arrêt
itermax = 60; // idem
// Précision de la linéarisation approchée
epsilon = 1e-6;
// **********
// Fonctions
// **********
exec('fonctions_communes.sce', -1)
function [e] = res(Yexp, Ycal)
e = sqrt(sum((Yexp-Ycal).^2));
endfunction
function [A, R] = gaussnewton(f, X, Yexp, A0, imax, epsilon)
// A : jeu de paramètres optimisé par régression (vecteur)
// R : liste des facteurs de qualité de la régression
// pour chaque étape (vecteur)
// X : variable explicative (vecteur)
// Yexp : variable expliquée, valeurs mesurées (vecteur)
// A0 : paramètres d'initialisation du modèle (vecteur)
// epsilon : valeur d'arrêt (scalaire)
k = 1; // facteur d'amortissement initial, <=1,
// évite la divergence
n = size(X,'*');
e0 = sqrt(sum(Yexp.^2)); // normalisation du facteur de qualité
Ycal = f(A0, X); // modèle initial
R(1) = res(Yexp, Ycal)/e0; // facteur de qualité initial
disp('i = 1 ; k = 1 ; R = '+string(R(1))) // affichage param initiaux
i = 1;
B = A0;
subplot(2,1,1)
plot2d(X, Yexp, rect=[-3, -2, 3, 12])
plot(X, Ycal, "-r")
xstring(-2.8, -1.5, string(B))
subplot(2,1,2)
plot2d(R, rect=[1, 0, 10, 1])
xstring(1.2, 0.1, 'α = '+string(k)+' ; R = '+string(R(i)))
nom = 'picassym'+string(i)+'.gif';
xs2gif(0,nom)
drapeau = %t;
while (i < imax) & drapeau // teste la convergence globale
i = i+1;
deltay = Yexp - Ycal;
J = linearisation_approchee(f, B, X, epsilon); // matrice jacobienne
tJ = J'; // transposée
deltap0 = inv((tJ*J))*tJ*deltay;
drapeau2 = %t // pour une 1re exécution
while drapeau2 & (k>0.1) // teste la divergence sur 1 étape
deltap = k*deltap0;
Bnouveau = B + deltap';
Ycal = f(Bnouveau, X);
R(i) = res(Yexp, Ycal)/e0;
drapeau2 = (R(i) >= R(i-1)) // vrai si diverge
if drapeau2 then k = k*0.75; // atténue si diverge
else k0 = k; // pour affichage de la valeur
k = (1 + k)/2; // réduit l'atténuation si converge
end
end
B = Bnouveau;
drapeau = abs(R(i-1) - R(i)) > epsilon
clf;
subplot(2,1,1)
plot2d(X, Yexp, rect=[-3, -2, 3, 12])
plot(X, Ycal, "-r")
xstring(-2.8, -1.5, string(B))
subplot(2,1,2)
plot2d(R, rect=[1, 0, 10, 1])
xstring(1.2, 0.1, 'α = '+string(k0)+' ; R = '+string(R(i)))
nom = 'picassym'+string(i)+'.gif';
xs2gif(0,nom)
// disp('i = '+string(i)+' ; k = '+string(k0)+' ; R = '+string(R(i)))
end
A = B;
endfunction
// **********
// Programme principal
// **********
// lecture des données
donnees = read('pic_gauss_dissym_bruite.txt',-1,2);
// carcatéristiques des données
Xdef = donnees(:,1);
Ydef = donnees(:,2);
// Ainit = [-0.03, 9.7, 8*((0.84 - 0.03)/2.35)^2, 8*((0.45 + 0.03)/2.35)^2];
Ainit = [1, 1, 1, 1];
// Régression
tic();
[Aopt, Rnr] =...
gaussnewton(gauss_dissym, Xdef, Ydef,...
Ainit, itermax, precision)
t = toc();
// Courbe calculée
Yopt = gauss_dissym(Aopt, Xdef);
// Affichage
print(%io(2),Ainit)
print(%io(2),Aopt)
print(%io(2),t)
clf
subplot(2,1,1)
plot(Xdef, Ydef, "-b")
plot(Xdef, Yopt, "-r")
subplot(2,1,2)
plot(Rnr)
Licensiering
Jag, upphovsrättsinnehavaren av detta verk, publicerar härmed det under följande licenser:

|
Tillstånd ges att kopiera, distribuera och/eller modifiera detta dokument under villkoren i GNU Free Documentation License, Version 1.2 eller senare version publicerad av Free Software Foundation, utan oföränderliga avsnitt, framsidestexter eller baksidestexter. En kopia av licensen ingår i avsnittet GNU Free Documentation License.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
Denna fil har gjorts tillgänglig under licenserna Creative Commons Erkännande-DelaLika 3.0 Unported, 2.5 Generisk, 2.0 Generisk och 1.0 Generisk.
- Du är fri:
- att dela – att kopiera, distribuera och sända verket
- att remixa – att skapa bearbetningar
- På följande villkor:
- erkännande – Du måste ge lämpligt erkännande, ange en länk till licensen och indikera om ändringar har gjorts. Du får göra det på ett lämpligt sätt, men inte på ett sätt som antyder att licensgivaren stödjer dig eller din användning.
- dela lika – Om du remixar, transformerar eller bygger vidare på materialet måste du distribuera dina bidrag under samma eller en kompatibel licens som originalet.
Du får själv välja den licens du vill använda.
Bildtexter
Ingen bildtext har definierats
Objekt som porträtteras i den här filen
motiv
Denna egenskap har ett värde, men det är okänt
5 december 2012
image/gif
Filhistorik
Klicka på ett datum/klockslag för att se filen som den såg ut då.
| Datum/Tid | Miniatyrbild | Dimensioner | Användare | Kommentar | |
|---|---|---|---|---|---|
| nuvarande | 5 december 2012 kl. 14.13 | 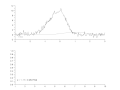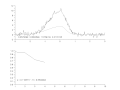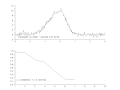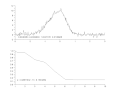 | 610 × 460 (22 kbyte) | wikimediacommons>Cdang | {{Information |Description ={{en|1=alpha (damping factor) value corrected}} |Source ={{own}} |Author =Cdang |Date = |Permission = |other_versions = }} |
Filanvändning
Följande sida använder den här filen: